제3의 고체, 준결정의 발견

정5각형만으로 축구공을 만들 수 있을까? 아무리 조합해도 축구공은커녕 평면조차 채울 수 없다. 평면 공간을 빈틈없이 꽉 채울 수 있는 모양은 따로 있다. 정6각형, 정4각형, 정3각형이다. 이 모양을 배열하면 주기적인 모양이 나타난다. 정6각형은 내각이 120°이므로 평면에 배열하면 같은 모양이 3번 나타난다. 정4각형은 4번, 정3각형은 6번 나타난다. 이렇게 한 도형을 360° 회전할 때 같은 모양이 반복되는 구조를 ‘대칭구조’라고 부른다. 즉, 정6각형은 3회, 정4각형은 4회, 정3각형은 6회 대칭구조다. 그러나 정5각형은 아무리 애를 써도 대칭구조를 나타낼 수 없다(정5각형의 내각은 108°다).    소금이나 금속 같은 고체도 원자나 원자군이 일정한 모양으로 연속해서 배열된 물질이다. 전자현미경으로 보면 원자나 원자군이 대칭구조를 이루며 주기적으로 배열돼 공간을 꽉 채운 모양이 나타난다. 이런 물질이 ‘결정질 물질’이다. 만약 원자가 규칙적인 배열 없이 무작위로 섞여 있다면 ‘비정질 물질’이라고 부른다. 유리가 대표적이다. 즉 고체는 결정질 물질 아니면 비정질 물질 둘 중 하나로 알려져 있었다.     준결정 물질을 발견하다 그러나 “고체의 결정 속 원자가 5회 대칭구조로 배열됐다”고 주장하는 과학자가 나타났다. 정5각형으로 축구공을 만들었다는 것과 마찬가지인 셈이다. 주인공은 바로 단 대니얼 셰시트먼(Daniel Shechtman, 1941~) 이스라엘공대 교수. 처음에는 이단시되며 학계에서 쫓겨나기까지 했으나 후에 이 주장은 사실로 밝혀졌다.

대니얼 셰시트먼 · 1941년 이스라엘 텔아비브 출생 · 이스라엘공대(테크니온) 공학박사 · 현재 이스라엘 공대 석좌교수 · 미국 아이오와주립대 교수, 미국 에너지부(DOE) 산하 에임스연구소 연구원   겸직 · 2011년 노벨 화학상 수상자

 

그가 발견한 것은 결정질 물질과 비정질 물질의 중간인 준결정 물질이었다. 셰시트먼 교수는 준결정을 발견한 공로로 올해 노벨 화학상의 영예를 안았다. 금속재료 분야에서 노벨상 수상자가 나온 것은 이번이 처음이다. 지난 2007년 9월 셰시트먼 교수는 필자가 단장을 맡고 있는 연세대 준결정재료창의연구단을 방문한 적이 있다. 필자는 준결정을 발견했을 때의 이야기를 직접 들을 수 있었다. 거의 30년이 지난 이야기지만 셰시트먼 교수는 준결정을 발견한 그 순간을 생생히 기억하고 있었다.   1982년 4월 8일, 셰시트먼 교수가 미국 국립표준기술연구소(NIST, 당시 국립표준국)에서 방문연구원으로 있을 때다. 그는 그날도 어김없이 전자현미경으로 합금의 결정구조를 관찰하고 있었다. 중량기준으로 20%의 망간이 섞여있는 알루미늄 합금의 결정구조를 관찰하던 중 원자 배열이 이상하다는 것을 발견했다. 전자현미경으로 관찰한 회절패턴이 5회 대칭구조를 이루고 있는 것이다. 5회 대칭구조를 가지는 결정은 없다는 게 당시의 정설이었다.

 

반복성이 없는 단위 도형이라도 2가지 종류를 이용하면 평면 공간을 모두 채울 수 있다. 이런 펜로즈 타일링의 개념을 도입하면 준결정의 구조를 풀 수 있다.

셰시트먼 교수 자신도 실험 결과를 믿을 수 없었다. 그러나 같은 실험을 반복하고, 다른 각도에서 찍어 봐도 마찬가지였다. 고민 끝에 동료들에게 이 결과를 말했지만 믿는 사람은 아무도 없었다. 심지어 그의 소속 연구실은 연구실의 명예를 실추시켰다며 그를 퇴출시켰다. 셰시트먼 교수는 어쩔 수 없이 다른 연구실로 옮겨야 했다. 그러나 셰시트먼 교수는 소신을 굽히지 않았다. 결국 그는 이 결과를 미국 국립표준기술연구소의 존 칸(John Cahn, 1928~) 박사와 함께 물리학 분야 과학지인 ‘피지컬 리뷰 레터스’에 발표했다. 이후 학계에서는 이런 원자 구조를 가진 결정이 있는지를 확인하려는 논쟁이 벌어졌다. 불과 한 달 뒤 물리학자 폴 스타인하르트(Paul Steinhardt, 1952~)와 도브 르바인(Dov Levine)은 이 결정 구조를 ‘펜로즈 타일링’의 패턴 구조로 설명할 수 있다는 사실을 같은 과학지에 발표했다.   또 다른 종류의 준결정을 찾는 연구도 본격적으로 시작됐다. 과학자들은 여러 금속 합금에서 8회, 10회, 12회 대칭구조를 더 찾았다. 이들 모두 당시에는 고체의 결정을 이룰 수 없다고 알려진 구조다. 준결정에 속하는 금속 합금의 종류는 점점 많아졌다. 새로운 준결정이 계속 발견되며 결국 결정학 교과서를 새로 써야 했다.

 

준결정 연구는 여전히 활발하게 진행 중이다. 국제준결정학회 같은 대규모 국제학회도 꾸준히 열리고 있다. 새로운 준결정 구조를 발견하는 것은 아마 끝이 없을 것이다. 지금도 어느 연구자의 책상 서랍 속에 풀지 못한 수수께끼로 남은 채 들어 있을 것이다. 준결정을 발견한 것은 학문적으로 큰 성과일 뿐 아니라 연구자들에게 좋은 교훈을 남겼다. 연구를 하다가 기존 결과와 다른 결과를 얻더라도 그냥 지나치지 말고 오히려 소중히 여겨야 한다는 것이다. 준결정도 처음 발견했을 때는 당시의 결정학 이론과 너무나 달라 셰시트먼 교수의 학설을 반대하는 목소리가 만만치 않았다. 심지어 노벨상을 두 번 수상한 결정학계의 대가, 라이너스 폴링(Linus Pauling, 1901~1994)이 앞장섰다. 하지만 셰시트먼 교수는 끝까지 주장을 포기하지 않았다. 셰시트먼 교수는 실험을 반복하며 계속 과학적 의미를 찾아냈다. 그 결과 새로운 소재를 발견하고 노벨상까지 탈 수 있었던 것이다.

 

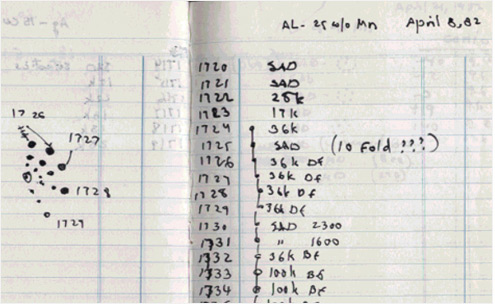
셰시트먼 교수의 실험노트. 결정이 특이한 것을 관찰하고 그 구조를 풀기 위해 고민한 흔적이 남았다.

결정학계의 대가인 라이너스 폴링은 준결정을 인정하지 않았다. 폴링은 “준결정은 없지만 준과학자가 있다”며 셰시트먼 교수를 비판했다.

 

 

원하는 성질의 금속을 디자인하다 물질의 구조를 알면 기계적, 전자기적 특성을 유추할 수 있다. 준결정은 그 이름에서 알 수 있듯 구조가 결정질 물질과 비정질 물질의 중간이다. 따라서 두 물질의 성질을 모두 갖고 있다. 결정질 물질처럼 단단하면서도 비정질 물질처럼 열이나 전기를 잘 전달하지 않는다. 이런 특성을 이용해 준결정으로 면도날이나 프라이팬의 코팅재, 엔진을 보호하는 단열재 등을 만들 수 있다. 이렇게 준결정 자체를 이용할 수도 있지만 준결정의 구조만 빌려 금속합금을 새로 설계할 수도 있다. 결정의 구조에 따라 금속의 특성이 변하기 때문이다. 기존에 쓰던 금속합금이라도 구조를 바꾸면 새로운 재료로 탈바꿈한다. 결정의 구조를 그야말로 ‘타일을 붙이듯’ 만들면 새 소재가 탄생한다. 어떻게 붙이느냐에 따라 획기적인 소재를 얻을 수도 있다. 반대로 원하는 물성을 얻기 위해 새로운 구조를 디자인할 수도 있다. 준결정을 발견하기 전까지는 금속의 조성이나 제조공정을 바꿔 합금을 강하게 만드는 방법밖에 없었다. 그러나 이제 비행기나 자동차, 교량 어디에 쓸지에 따라 필요한 물성대로 금속을 생산할 수 있게 됐다. 준결정이 소재 분야의 패러다임을 완전히 바꾼 것이다.

 

준결정강화마그네슘 합금(왼쪽, 합금의 구조)은 가벼우면서도 단단해 초경량 비행기(오른쪽, 출처: gettyimages)의 재료로 쓸 수 있다.

 

 

필자도 이런 연구를 하는 과학자다. 필자는 마그네슘 합금이 준결정 구조를 이루도록 다시 만들었다. 마그네슘 합금은 알루미늄 합금보다 무게는 가벼우면서 강하기 때문에 더 많은 용도로 쓸 수 있다. 그러나 제품을 만들 때 원하는 형태로 제작하기가 어려워 널리 사용하지는 않았다. 필자는 이 마그네슘 합금의 결정 구조를 새로 만들기로 했다. 그 결과 일반 마그네슘 합금과 다른 성질을 얻을 수 있었다. 1.5배 단단하면서도 30%나 가벼워졌다. 게다가 2배 잘 늘어나고 400℃가 넘는 고온에서도 마음대로 형태를 바꿀 수 있었다. 고온에서 변형해 얼마든지 원하는 형태로 만들 수 있는 것이다.   새로 설계한 준결정 강화 마그네슘 합금을 휴대전화나 MP3 플레이어, 노트북, PC 등 소형 전자제품의 외장재로 개발했다. 가벼우면서도 튼튼하기 때문에 안성맞춤이었다. 앞으로는 초경량 비행기와 자동차에 쓸 예정이다. 그 밖에 이 합금은 대전차 미사일, 우주왕복선 등 방위산업이나 우주개발에도 이용할 수 있다. 이렇게 준결정을 이용하면 기존 재료로 만들기 어려운 제품을 쉽게 만들 수 있다. 앞으로도 준결정은 무궁무진한 재료의 세계로 우리를 안내할 것이다.

 

 

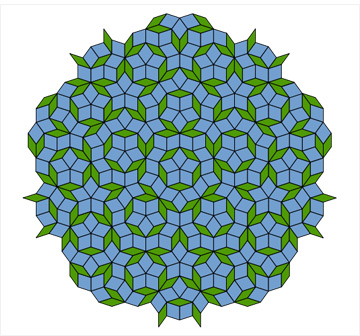
1. 펜로즈 타일링

   펜로즈 타일링은 벽지나 실내 바닥의 타일링 도안으로 흔히 사용돼 왔다. 펜로즈 타일링 속 패턴은 1973년 영국의 과학자 로저 펜로즈(영화 인셉션 속 ‘펜로즈 계단’을 고안한 이론물리학자)가 수학적으로 증명했다. 준결정이 발견되기 10년 전의 일이다. 평면을 같은 크기의 5각형으로 채우는 것은 불가능하지만, 두 개의 다른 마름모꼴을 일정한 법칙에 따라 배열하면 그 배열이 5회 대칭구조를 나타낸다는 것이다. 배열도형 전체로 보면 각각의 마름모꼴은 불규칙하게 들어서 있어 주기성은 없다. 그러나 분명 5회 대칭구조가 보인다.

    

   셰시트먼 교수가 발견한 준결정 구조는 이런 펜로즈 타일링의 개념을 도입해 풀 수 있다. 즉, 두 가지 다른 형태의 도형으로 공간을 채워 3차원으로 나타내면 5회의 대칭 구조가 가능하다는 것이다. 원자 배열에 주기성은 보이지 않지만 결정을 이룰 수 있다. 결정은 한 종류의 도형으로 이뤄졌다는 기존의 결정학 이론을 뛰어 넘는 것이다. 이 결정에 ‘준결정(quasicrystal)’이라는 이름을 붙였다. 결정질 물질과 비정질 물질의 중간적인 구조를 갖는다는 의미에서다.

 

 

 

글 김도향 / 연세대 교수

서울대 공대에서 학사와 석사를 마치고 영국 옥스포드대에서 박사학위를 받았다. KIST 선임연구원과 포항공대 조교수를 거쳐 1995년부터 현재까지 연세대에서 교수(준결정재료창의연구단 단장)로 재직 중이다. 500여 편의 금속재료 관련 연구 논문을 발표했고 ‘알루미늄 응용기술의 이해와 활용’ 등의 저서가 있다.

자료제공과학동아

이미지 동아일보, 노벨재단, 김도향

발행일  2011.11.11