
주기율표는 원소들을 원자번호 순서에 따라 배열하되, 비슷한 성질의 원소들이 같은 세로 줄(족)에 오도록 배열한 표이다. 따라서 우리는 주기율표와 원소 성질의 규칙적이고 주기적 변화 경향으로부터 원소들의 성질을 예측할 수 있다. 오늘날 사용되는 것과 같은 주기율표는 1869년에 러시아 화학자 멘델레예프(Dmitri Mendeleev, 1834~1907)가 원소들을 원자량 순서로 배열하여 처음 만들었는데, 그는 원소 성질의 규칙성과 주기성이 어떤 것에서 연유되는지는 알지 못하였으나, 지금은 그것이 원자들의 전자 배치에 의한 것으로 파악하고 있다. 원자의 전자 배치가 원소의 물리 및 화학적 성질에 어떻게 연관되는지, 그리고 원소들의 성질이 주기율표에서 어떤 경향을 갖고 변하는지를 살펴보기로 한다.
원자의 전자배치와 이의 주기성
원소 성질의 규칙성과 주기성은 원자의 전자배치를 분석하는 것으로 설명될 수 있다. 원자의 전자배치에 대해서는 네이버캐스트 ‘원소와 원자’ 에서 어느 정도 소개되었으므로, 이번 글에서는 원소의 주기적 성질을 설명하는데 필요한 내용을 소개하고, 원자의 전자배치의 규칙적이고 주기적 변화를 보여주고자 한다.
원자, 분자, 소립자 등의 미시적 대상에 적용되는 양자역학적 분석에 따르면, 원자에서 전자들의 공간적 분포, 에너지, 원자 성질 등을 결정하는 전자배치는 4개의 양자수 n, ℓ, m, ms 에 의해 결정된다. 주양자수 n은 1, 2, 3, 4, … 과 같은 양의 정수이다. 주양자수에 의해 구별되는 전자 궤도(orbital, 오비탈)를 전자껍질(electron shell)이라 부르는데, n =1, 2, 3, 4, …인 전자껍질을 각각 K, L, M, N, …껍질이라 부르기도 한다. 주어진 주양자수 n에서는 0부터 n-1까지의 정수인 n개의 방위양자수(또는 각운동량 양자수라 부름) ℓ 이 허용되는데, ℓ = 0, 1, 2, 3, …인 전자 궤도를 각각 s, p, d, f,…궤도 또는 부껍질(subshell)이라 부른다. 또 주어진 ℓ 에서는 -ℓ부터 +ℓ까지의 정수(0 포함)인 (2ℓ+1)개의 자기양자수(m)가 허용된다. 그리고, 각각의 주어진 (n, ℓ, m) 세트에서는 스핀양자수(ms)가 +1/2과 -1/2(또는 α와 β)인 두 가지 상태가 있다. 따라서 원자에 있는 각 전자의 양자 상태를 이들 4가지 양자수 (n, ℓ, m, ms)의 세트로 나타낼 수 있는데, 파울리의 배타 원리(Pauli exclusion principle)에 의하면 한 원자에 속하는 어떤 2 개의 전자도 동일한 순간에 같은 세트의 양자수를 가질 수 없다. 따라서 s, p, d, f 부껍질에는 각각 최대로 2x(2ℓ +1)개의 전자, 즉 2, 6, 10, 14개의 전자가 있을 수 있으며, n = 1, 2, 3, 4, …인 전자껍질에는 각각 2, 8, 18, 32, … 즉 2n2개의 전자가 있을 수 있다.
1개의 전자만 있는 수소 유사 원자(hydrogen-like atom; 원자핵과 1개의 전자로 이루어진 원자로, 수소를 제외하고는 사실상 (Z-1)의 양전하를 갖는 이온이며, 예로 He+, Li2+ 등이 있다)의 전자 에너지(EH)와 평균 전자 궤도 반경(<r>H)은 주양자수 n와 원자핵 전하(원자번호, Z)의 함수로 다음과 같이 나타낼 수 있다(에너지는 전자가 원자핵에서 무한히 떨어진 경우의 에너지를 0으로 정해 기준으로 삼는다).

여러 개의 전자를 갖는 원자나 이온에서의 전자 에너지는 n에 의해 주로 결정되나 ℓ 에도 약간 의존하는데, 같은 n에서는 ℓ 값이 클수록 약간 커진다. 바닥 상태의 원자에서는 에너지가 낮은 상태부터 전자가 채워지는데, 그 순서는 (n + ℓ)의 순서이며, (n + l)이 같은 경우는 n이 작은 궤도부터 먼저 채워진다. 따라서 전자가 채워지는 궤도의 순서는 1s<2s<2p<3s<3p<4s<3d<4p<5s<4d<5p<6s<4f<5d<6p<7s<5f<6d<7p<… 가 되는데, 이를 원자의 전자배치 원리(Aufbau principle) 또는 마델룽 규칙(Madelung rule)이라 한다.
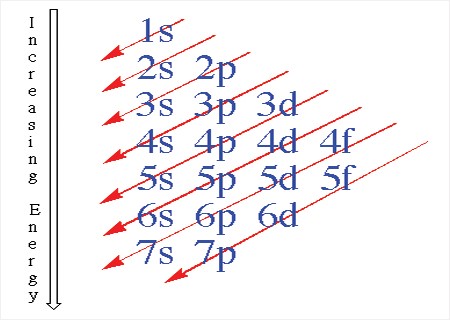
마델룽 규칙에 따른 원자의 전자배치 순서.
그러나 마델룽 규칙은 어디까지나 근사적인 것이고, 많은 수의 전자를 갖는 원자에서는 이에서 벗어나는 것이 흔히 발견된다. 이들 원자의 전자배치는 보다 정교한 양자역학적 계산과 분광학적 실험 결과를 분석하여 얻을 수 있는데, 아래 표는 원자들의 전자 배치를 정리한 것이다.
*4주기 6족 원소 24Cr은 [Ar]3d54s1이다. **[Kr]4dN-15s1의 전자배치를 갖는 원소들은 5족의 41Nb, 6족의 42Mo, 8족의 44Ru, 9족의 45Rh이다.
+란타넘족 원소(원자번호 57-71)에서 57La는 [Xe]5d16s2, 58Ce는 [Xe]4f15d16s2이고, 59~70번(64Gd 제외) 원소는 [Xe]4fx6s2로 x가 3에서 14까지(8제외) 차례로 채워지며, 64Gd는 [Xe]4f75d16s2. 71Lu는 [Xe]4f145d16s2이다.
++악티늄족 원소(원자번호 89~103)에서 89Ac은 [Rn]6d17s2, 90Th은 [Rn]6d27s2, 91Pa는 [Rn]5f26d17s2, 92U는 [Rn]5f36d17s2, 93Np는 [Rn]5f46d17s2이고, 94~102번(96Cm 제외) 원소는 [Rn]5fx7s2로 x가 6에서 14(8제외)까지 차례로 채워지며, 96Cm는 [Rn]5f76d17s2. 103Lr은 [Rn]5f147s27p1이다.
원자들의 전자배치를 보면, 같은 족의 원소들은 맨 바깥(최외각) 전자 껍질(흔히 원자가 껍질(valance shell)이라고 한다)의 주양자수만 다를 뿐 전자 배치는 거의 같음을 볼 수 있다. 즉, 주기율표의 같은 족에서 위에서 아래로 갈 때 최외각 껍질의 전자 수와 부껍질의 종류는 변하지 않고 주양자수만 주기번호와 함께 커진다. 한편, 같은 주기의 원소들, 특히 주족원소(1, 2, 13~18족 원소)들에서는 주기율표에서 왼쪽에서 오른쪽으로 갈수록 같은 최외각 전자 껍질의 전자수가 증가함을 볼 수 있다. 이러한 점들이 주기율표에서 원소 성질의 주기성에 대한 바탕이 된다.
유효 핵전하(Effective Nuclear Charge)와 슬레이터 규칙(Slater’s rule)
원자는 중심에 전하를 띠지 않은 중성자와 원자번호(Z)와 같은 수의 양전하를 띤 양성자로 이루어진 원자핵이 있고, 그 주위에 음전하를 띤 전자가 있다. 전자들은 원자핵의 양전하에 의해 정전기적으로 끌리는데, 수소를 제외한 원자들은 여러 개의 전자를 갖는 다(多)전자 원자여서, 이들 원자에 있는 전자, 특히 높은 궤도의 전자는 보다 낮은 궤도의 전자들에 의한 가리움효과(차폐효과, shielding effect) 때문에 원자핵의 전하를 그 크기 그대로 느끼지 못하고 더 작게 느끼게 된다. 전자가 실제로 느끼는 원자핵의 전하를 유효 핵전하(Zeff)라 하는데, 어떤 전자에 대한 유효 핵전자는 원자핵 전하(원자번호 Z)에서 다른 전자들이 일으키는 가리움 효과(s)를 뺀 값, 즉 Zeff=Z-s로 주어진다. s를 전자의 가리움상수(shielding constant)라 하는데, 해당 전자를 제외한 모든 전자의 가리움 상수의 합이다. 만약 내부 전자들에 의한 원자핵 전하의 가리움이 완벽하다면, 최외각 껍질에 있는 전자에 대한 유효 핵전하는 원자번호에서 내부전자의 수를 뺀 값이 될 것이나, 실제는 가리움이 완벽하지 않기 때문에 이보다는 약간 큰 값이 된다.
유효 핵전하는 1930년에 슬레이터(John C. Slater, 1900~1976))가 제안한 슬레이터 규칙(Slater’s rule)을 사용하여 가리움 상수 s를 구해서 얻는 것이 보통이다. 슬레이터 규칙은;
(1) 유효 핵전하를 구하고자 하는 해당 전자(이하에서는 그냥 ‘해당 전자’라 한다)와 같은 부껍질에 있는 전자의 가리움 상수는 0.35이다. 단 1s 전자의 가리움 상수는 0.3이다. 같은 주양자수를 갖는 s와 p 전자는 같은 부껍질에 있는 것으로 본다.
(2) 해당 전자가 s나 p 전자일 경우,주양자수가 1 적은 전자에 의한 가리움 상수는 0.85이고, 주양자수가 1보다 더 적은 전자에 의한 가리움 상수는 모두 1이다.
(3) 해당 전자가 d 또는 f 전자일 경우, 주양자수가 작거나 혹은 같은 주양자수를 갖지만 방위양자수가 작은 전자에 의한 가리움 상수는 모두 1이다.
이를 원자번호 26인 철(Fe: 전자배치 1s22s22p63s23p63d64s2)에 대해 적용해 보면, 4s 전자에 대한 가리움 상수는 22.25(=0.35x1 + 0.85x14 + 1.00x10)이 되고, Zeff는 3.75(=26-22.25)가 된다. 또 3d 전자에 대한 가리움 상수는 19.75(=0.35x5 + 1.00x18)가 되고, Zeff는 6.25 (=26-19.75)가 된다.
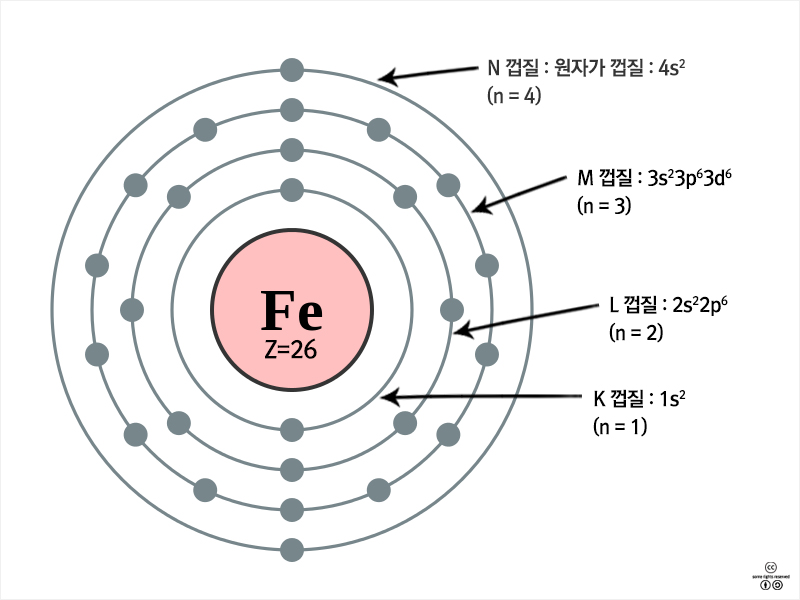
철(Fe) 원자의 전자배치 모형. 내부 전자(K~M 껍질의 전자)들의 가리움 효과가 완벽하다면, 4s 전자에 대한 유효 핵전하(Zeff)는 2가 되어야 하나, 슬레이트 규칙에 따른 Zeff는 3.75로 계산된다. <출처 : (cc) Pumbaa80 at wikimedia.org>
또 3주기 원소들의 맨 바깥 궤도 전자(3s 혹은 3p 전자)에 대해 계산해보면, Zeff는 Na(Z=11)는 2.2(=11-(0.85x8 + 1.00x2)), Mg(Z=12)는 2.85, Al(Z=13)은 3.5, Si(Z=14)는 4.15, P(Z=15)는 4.8, S(Z=16)는 5.45, Cl(Z=17)은 6.1. Ar(Z=18)은 6.75로, 주기율표에서 왼쪽에서 오른쪽으로 갈수록 0.65씩 커진다. 또 1족 원소들의 최외각 전자 껍질에 있는 전자(ns1)에 대해 Zeff를 계산해보면 Li(Z=3)은 1.3이고, Na 이후는 2.2로 같다.
한편, 같은 주양자수 n를 갖는 전자 궤도에 대해서는, Zeff를 Zeff = <r>H/<r>, 즉 수소 유사 원자의 평균 궤도 반경(<r>H)과 실제 원자의 평균 궤도 반경(<r>)의 비로 나타낼 수 있다. 따라서 주기율표에서 같은 주기의 원자들에서는 왼쪽에서 오른쪽으로 갈수록 Zeff가 증가하므로, 최외각 전자 궤도의 <r>이 작아진다. 즉 최외각 전자가 원자핵에 보다 가까이 있다. 그리고, 최외각 전자 껍질에 있는 전자의 주양자수 n은 그 원자가 속한 주기번호와 같고, 이 전자에 대한 Zeff는 주기번호와 거의 무관하게 같으면서 <r>H는 n 의 제곱에 비례하므로, 같은 족의 원소들은 주기율표에서 위에서 아래로 갈수록 최외각 전자 껍질의 <r>이 커진다. 즉 최외각 전자가 원자핵에서 보다 멀리 떨어져 있다.
물리적 성질의 주기성
원자번호에 따라 주기적 변화를 보이는 물리적 성질에는 원자 반경과 부피, 원자의 이온화 에너지, 전자친화도, 전기음성도, 원소의 금속성 등이 있다.
원소의 원자 반경은 원자 크기의 척도로, 보통 원자핵에서 전자 구름 경계까지의 평균 거리이다. 그러나 전자 구름의 경계는 잘 정의되지 않으므로, 두 원자가 결합하지 않고 가장 가까이 접근할 수 있는 거리의 1/2인 반데르발스 반경(van der Waals radius)과 다른 원자와 공유결합을 할 때의 추정 반경인 공유결합반경(covalent radius)이 주로 사용된다.
원자반경은 최외각 전자껍질의 <r>과 밀접하게 연관된다. 같은 주기의 원소들에 대한 원자 반경을 살펴보면, 이들 원소들은 최외각 전자 껍질에 있는 전자의 주양자수는 같으면서 Zeff는 주기율표에서 왼쪽에서 오른쪽으로 갈수록 커지므로, 원자반경도 왼쪽에서 오른쪽으로 갈수록 대체로 작아진다. 같은 족에 있는 원소들의 경우에는, 위에서 아래로 갈수록 최외각 껍질의 주양자수는 커지나 Zeff는 거의 같으므로, 원자반경은 위에서 아래로 갈수록 대체로 커진다. 또한, 원자반경은 각 주기의 끝에 있는 비활성 기체(18족)에서 다음 주기의 첫 번째 원소인 알칼리 금속(1족)으로 가면서 크게 증가하는데, 이는 하나의 새로운 전자 껍질이 더해지기 때문으로 설명된다.
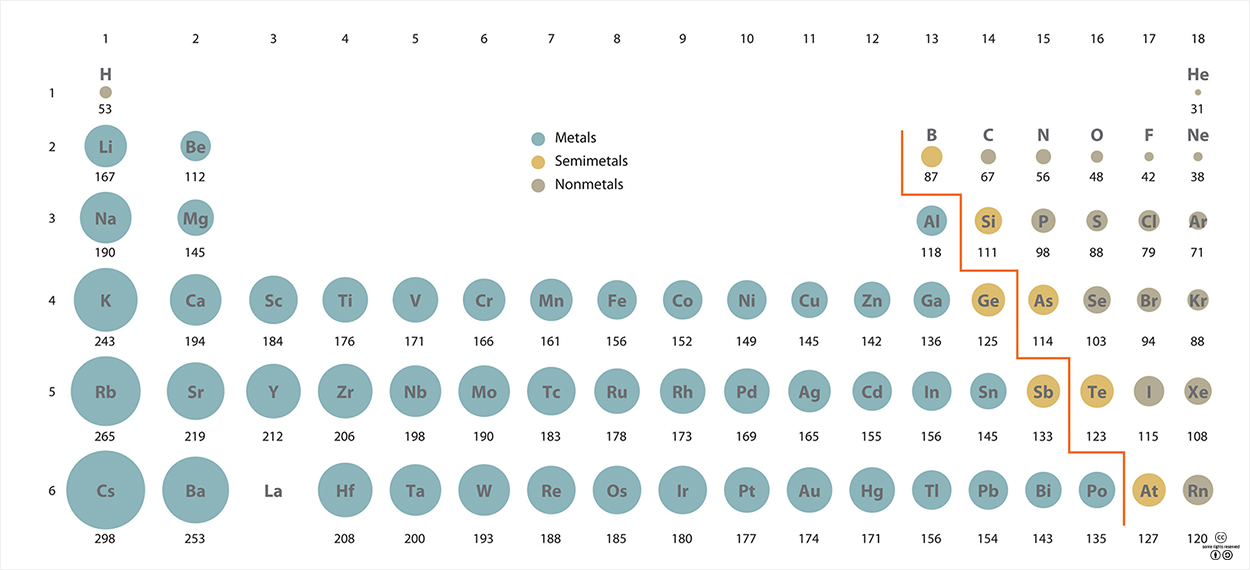
s, p, d-블럭 원자들의 상대적 크기. 숫자는 양자역학적 파동 함수에서 계산된 원자반경으로 단위는 pm(1pm=0.01 Å)이다. <출처 : (cc) Principles of General Chemistry>
전이금속의 경우에는 같은 주기에서 원자번호가 커질수록 원자반경이 줄어드는 정도가 주족원소에 비해 적은데, 이는 전이금속에서는 원자번호 증가에 따라 더해지는 전자가 내부 궤도에 들어가서 핵전하를 많이 가리기 때문에 원자번호 증가에 따른 이온 반경의 감소가 적게 나타나는 것으로 설명된다.
세륨(Ce, Z=58) 이후의 란타넘족 원소들에서는 원자번호가 커질수록 4f 전자가 차례로 채워지는데, 4f 전자는 이의 방향성 때문에 최외각의 6s 전자에 대한 가리움 효과가 완벽하지 않아 원자번호가 클수록 원자 반경이 감소한다. 특히 +3가 상태의 란타넘족 이온(Ln3+)들은 [Xe]4fx (x는 원자번호에 따라 0~14)의 전자배치를 갖는데, 이러한 4f 전자에 의한 원자핵 전하의 가리움이 덜 효과적이기 때문에 원자번호 증가에 따른 이온 반경의 감소가 현저하게 나타나서, 이를 란탄넘족 수축(lanthanide contraction)이라 한다. 란타넘족 이후의 6주기 원소들은 원자번호가 클수록 원자반경이 크게 감소하는데, 이 또한 완전히 채워진 4f14 전자 궤도에 의한 수축으로 설명된다. 이러한 원자 반경의 감소는 10족의 백금(Pt, Z=78)까지 관찰되는데, 백금 이후에는 상대론적 영향이 커져 원자반경이 오히려 커진다. 한편, 4족 이후의 6주기 원소들은 같은 족의 5주기 원소들과 비슷한 원자반경을 갖는데, 이는 6주기에서 추가로 더해지는 전자껍질의 영향이 란탄넘족 수축에 의해 거의 완전히 상쇄되기 때문인 것으로 설명된다. 4주기와 5주기의 채워진 d-궤도(d10)를 갖는 원소들도 d-블럭 수축의 영향으로 원자반경이 예상보다 작은데, 이러한 d-불럭 수축은 란탄넘족 수축보다는 덜 현저하다.
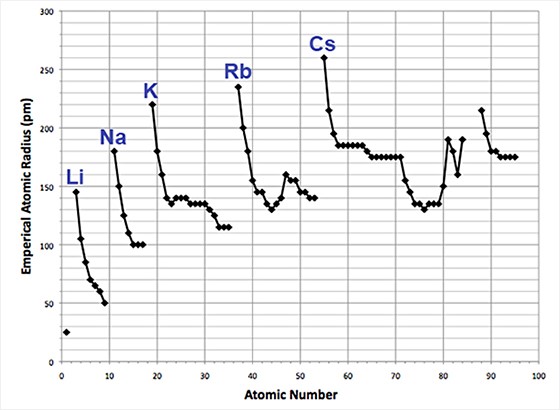
원소들의 원자번호에 따른 원자반경의 변화를 나타낸 그래프. 1964년에 슬레이터(Slater)가 결정이나 분자에서의 결합 길이에서 구한 데이터를 정리하여 발표한 것이다. <츨처 : (cc) StringTheory11 at Wikimedia.org>
원자 부피는 원자반경의 3제곱에 비례하므로, 원자반경과 마찬가지로 주기성을 보인다. 원자 부피의 주기성은 1870년에 마이어(Julius Lothar Meyer. 1830~1895)가 22개 원소에 대해 원자부피와 원자량의 상관 관계를 통해 처음 발표하였다.
원자의 이온화 에너지는 바닥 상태에 있는 기체 상태 원자에서 1개의 전자를 완전히 떼어내는데 필요한 최소의 에너지인데, 과거에는 이온화 전위(ionization potential)라고도 불렀다.

보통 위 식과 같이 중성 원자의 이온화 에너지를 그 원자의 첫 번째 이온화 에너지라 하고, (n-1)의 전하를 갖는 이온에서 전자 1개를 떼어내는데 필요한 에너지를 n 번째 이온화 에너지라 한다. 즉 두 번째와 세 번째 이온화 에너지는 각각 M+(g)와 M2+(g) 이온에서 전자 1개를 떼어내는데 필요한 최소의 에너지이다. 전자는 원자의 전자배치에서 에너지가 높은 것부터 떨어져 나가며, 따라서 (n+1) 번째 이온화 에너지는 n 번째 이온화 에너지 보다 항상 크다. 원자는 이온화 에너지가 작을수록 기체 상태에서 쉽게 전자를 잃고 양이온이 된다.
이온화 에너지는 대체로 떨어져 나가는 전자에 대한 유효 핵전하 Zeff에 비례하고, 전자가 들어있는 궤도의 평균 반경에 반비례한다. 따라서 주기율표의 같은 주기에 있는 원소들의 첫 번째 이온화 에너지는 대체로 왼쪽에서 오른쪽으로 갈수록 커진다. 다만 맨 바깥 궤도의 전자배치가 ns2np1 또는 np4의 전자 배치를 갖는 원소(예로, 3주기 원소의 경우 각각 Al과 S)는 바로 앞의 원소(예로, 3주기의 경우 각각 Mg와 P)에 비해 이온화 에너지가 작은데, 이는 최외각의 ns2 또는 np3 전자 배치가 보다 안정하기 때문이다. 전이금속에서는 원자번호의 증가에 따른 이온화 에너지의 증가 정도가 작은데, 이는 앞에서 살펴본 원자반경에 대한 경우와 마찬가지이다.
완전히 채워진 전자 껍질을 갖는 비활성 기체 원소의 이온화 에너지는 매우 커서 전자를 떼어내기가 극히 어려우며, 비활성 기체와 같은 전자배치를 갖는 이온에서 전자를 떼어내는 경우도 마찬가지이다. 예로, 원자번호 11번인 Na(전자배치 [Ne]3s1)의 첫 번째 이온화 에너지는 496 kJ/mol인 반면 두 번째 이온화 에너지는 이보다 월등히 큰 4,560 kJ/mol이고, 원자번호 12번인 Mg([Ne]3s2)의 이온화 에너지는 첫 번째가 738 kJ/mol이고 두 번째는 1450 kJ/mol로 첫 번째의 약 2배인 반면, 세 번째 이온화 에너지는 7.730 kJ/mol로 두 번째의 약 5배가 된다.
원자의 전자친화도(electron affinity)는 바닥 상태에 있는 기체 상태 원자에 1개의 전자를 더해 –1가 음이온(M-)을 만들 때 방출되는 에너지이다. 따라서, 이 값이 클수록 원자는 쉽게 음이온이 된다.

비활성 기체(18족) 원소들의 전자친화도는 잘 알려져 있지 않는데, 아주 작은 양(+)의 값이거나 또는 음(-)의 값일 것으로 짐작된다. 전자친화도는 주기율표의 같은 주기에서는 대체로 왼쪽에서 오른쪽으로 갈수록 증가한다. 17족(할로겐 족) 원소들은 전자 1개가 더해지면 비활성 기체와 같은 안정한 전자배치를 가지므로, 특히 크다. 그리고 2족 원소들은 전자친화도가 작은데, 이는 이들 원소가 채워진 s 부껍질을 가져 안정하기 때문이다. 2주기와 3주기의 5족 원소(N와 P)들도 앞 뒤의 원소들에 비해 작은 값을 갖는데, 이는 3개의 전자를 갖는 p 부껍질이 상대적으로 안정하기 때문이다. 같은 족에서는 위에서 아래로 갈수록 대체로 감소하는데, 이는 원자핵에서 보다 멀리 떨어진 전자 궤도에 전자가 들어가므로 원자핵 전하에 의해 보다 덜 끌리기 때문으로 볼 수 있다.
전기음성도(χ)는 원자가 전자를 끌어 당기는 척도로, 1932년에 폴링(Linus Paouling)이 처음 제안하였다. 1934년에 멀리컨(R. S. Mulliken)은 eV 단위로 나타낸 각 원자의 이온화 에너지와 전자친화도의 평균값을 전기음성도로 정의하기도 하였으며, 이후 여러 척도가 제안되었다. 현재 흔히 사용되는 전기음성도는 폴링이 당초 제안하였던 것과 같은 것인데, A와 B 두 원소의 전기음성도 차이는 다음과 같이 정의된다..
![\quad \quad \quad \quad \quad \quad \chi \left( A \right) -\chi \left( B \right) =\combi ^{ -1/2 }{ \left( eV \right) }\combi ^{ 1/2 }{ \left\{ \combi _{ d }{ E }\left( AB \right) +\left[ \combi _{ d }{ E }\left( AA \right) +\combi _{ d }{ E }\left( BB \right) \right] \right\} }](http://static.naver.net/ncc//equation/09/20/20140523142009406.png)
여기서 Ed는 해당 분자의 결합 해리 에너지(단위는 eV)이다. 폴링이 정한 척도의 기준으로는, 수소 원자의 전기음성도를 당초에는 2.10으로 하였으나, 지금은 2.20로 삼는다. 원소들의 전기음성도는 0.7에서 3.98사이의 값들인데, 프랑슘(87Fr)이 가장 작고, 플루오린(9F)이 가장 크다. 주기율표에서는 대체로 같은 주기에서는 왼쪽으로 오른쪽으로 갈수록 커지고, 같은 족에서는 위에서 아래로 갈수록 작아진다. 전이금속 원소들에서는 다른 물리적 성질에서와 마찬가지로, 이들 경향에서 벗어나는 경우가 많다.
원소들은 이온화 에너지, 전자친화도, 전기음성도가 작을수록 금속성이 커지며, 역으로 비금속성은 작아진다. 이에 따라, 금속성은 대체로 주기율표에서 왼쪽에서 오른쪽으로 갈수록 작아지고, 위에서 아래로 갈수록 커진다. 즉, 왼쪽 아래에서 오른쪽 위로 대각선 방향으로 갈수록 금속성이 작아진다. 따라서 주기율표의 왼쪽 맨 아래에 있는 세슘(Cs)이나 프랑슘(Fr)이 금속성이 가장 크고, 오른쪽 위에 있는 산소(O), 플루오린(F), 염소(Cl) 등이 비금속성이 가장 크다. 원소는 금속 성질이 크면 쉽게 양이온이 되고, 비금속성이 크면 쉽게 음이온이 된다. 다른 성질에서와 마찬가지로, 전이금속 원소들에서는 약간의 불규칙성이 보인다.
화학적 성질의 주기성
원소의 화학적 성질의 주기성은 앞서 보인 물리적 성질의 주기성보다는 덜 규칙적이고 더 복잡하다. 그러나 같은 족 원소들의 화학적 성질이 비슷하고 주기에 따라 일정한 경향성을 보인다는 점에서 화학적 성질의 주기성이 있음은 분명하다. 원소의 원자가와 산화상태에 대한 내용을 중심으로 화학적 성질의 주기성에 대해 살펴본다.
어떤 원자가 다른 원자(같은 또는 다른 종류 원자)와 결합할 수 있는 최대 화학결합의 수를 원자가(valance)라 한다. 원자가의 간단한 정의는 어떤 원자(M)의 이성분 수소화물(hydride, MHn)에 있는 수소 원자수(n) 또는 이성분 산화물(oxide, MmOn)에서 원자당 결합된 산소 원자수의 2배(즉, 2n/m)인데, 이러한 정의는 주로 주족원소에 적용된다. 원자가의 개념은 1852년에 영국 화학자 프랭크랜드(Edward Frankland, 1825~1899)가 처음 도입한 것인데, 멘델레예프는 1871년의 주기율표에서 원소들을 원자가에 따라 족을 나누어 구분하였다.
수소화물에서 보면, 1족과 2족 원소의 원자가 n은 족 번호와 같으며, 14족~18족 원소의 원자가 n는 n=18-N이 된다(N은 족 번호). 이를 3 주기 원소들에 적용하면, 수소화물의 화학식은 NaH, MgH2, CH4, NH3, H2O(또는 OH2), HF(또는 FH)가 되며, 18족 원소 Ne은 원자가가 0으로 수소화물을 만들지 않는다. 반면, 산소가 가장 많이 결합된 주족원소의 정규 산화물(과산화물이나 초과산화물이 아님)에서 보면, 원자가는 족 번호가 클수록 증가한다. 즉 1족 원소는 1(산화물 M2O), 2족 원소는 2(산화물 MO), 13족 원소는 3(산화물 M2O3), 14족 원소는 4(산화물 MO2), 15족 원소는 5(산화물 M2O5), 16족 원소는 6(산화물 MO3), 17족 원소는 7(산화물 M2O7)이다. 비활성 기체인 18족 원소의 원자가는 0이다.
원소의 족에 따른 원자가의 변화는 원자가 전자(valence electron)수와 옥텟 규칙(8전자 규칙, octet rule)으로 설명된다. 어떤 원자에서 화학 결합 형성에 관여할 수 있는 전자를 원자가 전자라 하며, 하나의 공유결합은 결합하는 두 원자가 한 개씩의 원자가 전자를 내어놓아 공유전자쌍을 공유함으로써 이루어진다. 어떤 한 원자 주위에 공유 전자를 포함하여 8개의 원자가 전자가 있게 되면 그 원자는 비활성 기체 원소와 같은 전자배치를 하여 안정하게 되는데, 이를 옥텟규칙이라 한다. 그러나 수소와 리튬 등의 경우는 원자핵 주위에 2개의 전자가 있으면 헬륨(He)과 같은 전자배치를 하여 안정화되며, 전이 금속 원소들은 d-궤도도 사용하므로 8 전자 규칙 대신 18전자 규칙(18-electron rule)이 적용된다. 주족원소의 원자가 전자는 최외각 전자 껍질에 있는 전자수가 된다. 이 때문에 최외각 전자 껍질을 원자가 껍질(valance shell)이라 부른다. 원자가 전자 수는 1족은 1개, 2족은 2개, 그리고 13~18족은 각각 3~8개가 된다. 18족 원소(비활성 기체)는 그 자체가 8개의 원자가 전자를 갖고 있으므로 화학적으로 안정한다. 전이금속 원소들의 경우에는 원자가 전자가 내부 껍질(d 또는 f 궤도)에 있을 수도 있어 정의하기 어려우나, 보통 최외각 s전자 2개를 원자가 전자로 보기도 한다.

탄소의 산화물인 이산화탄소. 탄소는 4개의 원자가 전자를 갖고 있는데, 6개의 원자가 전자를 갖는 산소 원자 2개와 각각 2 쌍의 전자를 공유하여 모든 원자들이 옥텟규칙을 만족한다. 이와 같은 분자 구조식을 루이스(Lewis) 점구조식이라 한다.
화합물에서 어떤 원소의 산화상태는 그 원자에 있을 것으로 생각되는 형식 전하의 양으로, 이를 숫자로 표시한 것을 산화수(oxidation number)라 한다. 산화상태, 즉 산화수는 아래 규칙에 따라 계산된다. (1) 결합되지 않은 원소의 산화상태는 0이다. (2) 단일 원자 이온의 상태상태는 이온의 전하수와 같다. (3) 대부분의 화합물에서 수소의 산화상태는 +1이고 산소의 산화상태는 -2이다. 다만, 활성 금속의 수소화물(예로 LiH, CaH2)에서의 수소의 산화상태는 -1이고, 과산화물(peroxide, 예로 H2O2, Na2O2)과 초과산화물(superoxide, 예로 NaO2)에서의 산소의 산화상태는 각각 -1과 -1/2이다. (4) 중성 분자에서 각 성분 원자의 산화 상태의 합은 0이며, 이온에서 각 성분 원자의 산화 상태의 합은 이온의 전하수와 같다. 황(S)의 예를 들면, H2S, S8, SO2, SO3, H2SO4에서 S의 산화상태는 각각 -2, 0, +4, +6, +6이다.
비활성 기체를 제외한 주족원소들이 갖는 최대 가능한 양(+)의 산화수는 그 원자의 원자가 전자수와 같으며, 이러한 최대 산화수에서 2씩 감소한 산화상태가 비교적 흔하다. 예로 17족 할로겐 원소들의 산화수는 보통 +7, +5, +3, +1이고, +6, +4, +2의 산화 상태를 갖는 화합물도 있다. 다만 플루오린은 전기음성도가 가장 큰 원소이므로, 다른 원소에 의해 산화되지 않아 양의 산화수를 갖는 화합물이 없다. 전이금속 원소들은 8족까지는 족 번호와 같은 수의 산화수를 갖는 화합물들이 흔하고, 9~12족 원소들은 주로 +1~+4의 산화 상태를 갖는다. 비금속 원소들은 다른 원자에서 전자를 받아 음(-)의 산화 상태를 갖는데, 산화수는 보통 -(8-원자가 전자수)가 된다. 란타넘족 원소들은 주로 +3의 산화상태를 가지며, 일부 원소에서는 +2와 +4의 산화상태도 관찰된다. 악티늄족 원소들은 주로 +3과 +4의 산화상태를 갖는데, 넵튜늄(Np), 플루토늄(Pu), 아메리슘(Am)은 +7까지의 높은 산화상태를 갖기도 한다. 개별 원소들이 어떤 산화상태를 갖는가에 대한 내용은 네이버캐스트에 실린 개별 원소들에 대한 글에서 언급되었다.
글쓴이는 이 글을 끝으로 지난 4년 가까운 기간 동안 총 123회에 걸쳐 네이버캐스트에 연재한 화학원소에 대한 글을 마친다. 그 동안 글쓴이의 글을 읽어준 모든 분들께 감사 드리며, 글쓴이의 글들이 화학과 원소들을 보다 잘 이해하고, 원소들에 대한 정보를 얻는데 계속 유용하게 이용되었으면 하는 마음 간절하다.

- 글
- 박준우 이화여대 명예교수(화학)
- 서울대학교 화학과를 졸업하고 템플대학교에서 박사학위를 받았다. 오랫동안 이화여대에서 화학을 연구하고 가르쳤다. 저서로 [인간과 사회와 함께한 과학기술 발전의 발자취]와 [아나스타스가 들려주는 녹색화학 이야기] 등이 있고, 역서로 [젊은 과학도에 드리는 조언] 등이 있다.
- 저자의 책 보러가기인물정보 더보기
'Natural science > 화 학' 카테고리의 다른 글
| Fermminum(Fm), 100-페르뮴 (0) | 2014.07.05 |
|---|---|
| 주기율표(Periodic Table) (0) | 2014.07.05 |
| Einsteinium(Es), 99-아인슈타인늄 (0) | 2013.11.22 |
| Californium(Cf),98- 캘리포늄(Cf) (0) | 2013.11.22 |
| Berkelium(Bk), 97-버클륨(Bk) (0) | 2013.11.22 |




